※사칙 연산(+, -, *, /)만 다룹니다.
논리회로는 귀찮아서 따로 그리지 않았습니다.
1. 반가산기와 전가산기
컴퓨터는 전가산기를 통해 덧셈을 수행합니다.
그 과정에서 반가산기를 사용하기에 반가산기를 포함하여 설명드립니다.
이진수 덧셈과 십진수 덧셈은 다를게 없습니다.
10진수 두 수 7과 4가 있다고 칩시다.
이 두 수의 이진수 덧셈과 십진수 덧셈과정을 봅시다.
각 수를 A와 B라고 부르겠습니다.
10진수인 경우
- A, B 각각 일의 자리부터 더한다.
- A의 현재 자릿수에 1을 B의 현재 자리수만큼 덧셈을 반복한다.
- 더하는 도중 현재 자릿수가 9를 초과할 시 현재 자릿수를 0으로 만들고 다음 자릿수를 1올림한다. (올림 발생)
- 올림 발생 후 나머지를 더한다.
이 네가지대로 더한다면 A가 7이고 B가 4니까
7에 1을 4번 더하는거니까
3번에서 나온것처럼 10이 되고
4번을 수행하면 11이 됩니다.
만약 A가 15여서 한쪽만 자릿수가 더 높아서 B의 십의 자리가 없다면?
A의 십의 자리에 B의 십의 자리를 0만큼 더하면 됩니다.
10진수에서 했던것 처럼 현재 자릿수 덧셈 공식을 똑같이 적용해봅시다.
2진수인 경우 (0111, 0100)
- A^0 와 B^0을 더한다(1 + 0) → 1
- A^1 와 B^1을 더한다(1 + 0) → 1
- A^2 와 B^2을 더한다(1 + 1) → 0 (올림 발생)
- A^3 와 B^3을 더한다(0 + 0 + 이전 올림) → 1
- 결과 1011 → 10진수 11
이 과정을 좀더 깊게 살펴봅시다.
| 7 | 4 | 합 | 올림 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
표를 보면 합이 0011, 올림이 0100이 됩니다.
합은 어떤 비트연산을 써야할까요?
XOR를 사용하면 될것 같군요. 따라서 식은 A ^ B가 되겠습니다.
올림은 어떤 비트연산을 써야할까요?
AND를 사용하면 될것 같군요. 따라서 식은 A & B가 되겠습니다.
그럼 10진수도 똑같이 해볼까요?
347과 921이 있다고 칩시다.
| 347 | 921 | 합 | 올림 |
| 7 | 1 | 8 | 0 |
| 4 | 2 | 6 | 0 |
| 3 | 9 | 2 | 1 |
| 0 | 0 | 0 | 0 |
여기서 똑같이 올림이 발생했으니 다음 자릿수로 올림을 적용하면?
1268 이라는 결과값이 나오게 됩니다!
2진수와 덧셈과정이 왜 똑같다는지 아시겠죠??
자 그럼 방금 보셨던 내용이 반가산기인데요.
반가산기(半加算器, half adder)는 이진수의 한자리수를 연산하고, 자리올림수는 자리올림수 출력(carry out)에 따라 출력한다. AND, OR, NOT의 세 가지 종류의 논리회로만으로 구성할 수 있다.
왜 반가산기(Hallf Adder)라고 불릴까요??
이유는 올림만 있지 그 올림을 실제로 적용시키지는 않기 때문인데요.
이제 올림을 실제로 적용시키는 전가산기의 과정을 봅시다.
전가산기 과정
- A와 B를 반가산기로 더한다.
- 반가산기로부터 나온 합(S)과 올림(C)을 반가산기로 더한다.
- 올림이 없을때까지 1-2를 반복한다.
자 이 과정을 표로 표현해봅시다.
| 7 | 4 | 이전 올림(Cin) | 합(S) | 올림(Cout) |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
첫 행부터 봐봅시다.
첫 번째 행 1 0 0 이기에 합이 1 올림 0
두 번째 행 1 0 0 이기에 합이 1 올림 0
세 번째 행 1 1 0 이기에 합이 0 올림 1
네 번째 행 0 0 1 이기에 합이 1 올림 0
최종 합 1011이 나오게 되는데
맨 처음 이전 올림은 당연히 없으니까 0
네 번째 행인 2^3 번째는 이전 올림이 있었기에 1이 되었죠
전가산기 과정 2번을 보면 합과 올림을 반가산기로 더한다는게
이전 올림(Cin)과 반가산기 합의 공식 A ^ B를 합하라는 것입니다.
여기서의 합의 공식은 A ^ B ^ Cin이 되겠습니다.
그렇다면 올림은 어떻게 될까요?
| A | B | 이전 올림(Cin) | 합(S) | 올림(Cout) |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
전가산기의 진리표입니다.
여기서의 이전 올림은 표의 현재 올림과 상관없습니다.
올림 공식을 어떻게 짜면 좋을까요?
처음 반가산기에서의 올림 공식은 A & B이었습니다.
유심히 살펴보면 A, B, Cin 이 셋중 두개 이상 1인 경우 올림이 발생합니다.
식으로 유도해보면
Cout = (A & B) | (A & C) | (B & C)
이렇게 식을 짤 수 있습니다.
따라서 합과 올림의 식은 다음과 같습니다.
S = A ^ B ^ Cin
Cout = A & B | A & C | B & C
2. 덧셈 구현
int Add(int a, int b) {
while (b != 0) {
int c = a & b;
a = a ^ b;
b = c << 1;
}
return a;
}c를 올림으로 사용하고
a를 합으로 사용하고
b를 마지막에 이전 올림을 적용 시켜줍니다.
이 과정을 반복하면 일반 + 연산과 동일한 기능을 하게되는데요.
설명드렸던 전가산기 과정을 보시면
- A, B를 반가산기로 더한다.
- 나온 합과 이전 올림을 더한다.
- 올림이 없을 때까지 반복한다.
int c = a & b가 올림
a = a ^ b 가 합
b = c << 1이 올림 적용
흐음.. Cin이 어디에 있는거지?? 라는 생각이 들면
while 2번째 부터 생각해 보세요
a는 이전 합을 구했고
b는 이전 올림을 적용한 상태입니다.
그래서 두 번째 반복부터 S = (a(A ^ B) ^ b(Cin)) 형태로써 완벽하게 합을 구할 수 있게 되는것이죠
이 과정을 b가 0이 아닐때 까지 == 올림이 없을 때까지 반복하면 덧셈 구현 끝입니다!
3. 뺄셈 구현
int Subtract(int a, int b) {
return Add(a, -b);
}뺄셈은 간단하죠 b를 음수로 만든 뒤 더하면 끝입니다.
물론 비트연산을 사용해 다르게 구현할 수 있습니다.
int Subtract(int a, int b) {
return Add(a, ~b + 1);
}다르게 구현하면 이 방식으로 구현할 수 있는데요
~ 기호는 not으로써 모든 0비트를 1로, 모든 1비트를 0으로 바꿉니다.
따라서 양수인 수는 음수, 음수인 수는 양수가 되는데요.
그렇다면 왜 1을 더하는가?
int 자료형의 범위를 보면 -2,147,483,648 ~ 2,147,483,647
최소값과 최대값이 절댓값 적용했을 때 1차이가 납니다.
그 이유는 0이 양수쪽에 포함되어있기 때문입니다.
따라서 not을 적용했을 때 1의 오차가 포함되어있기 때문에 1을 더해주면
~b + 1 == -b 식과 같기 때문에 a + ~b + 1을 해주면 뺄셈 구현 끝입니다.
4. 곱셈 구현
int Multiply(int a, int b) {
bool negativeResult = false;
if ((a < 0 && b > 0) || (a > 0 && b < 0))
negativeResult = true;
a = abs(a);
b = abs(b);
int t = 0;
while (b != 0) {
if (b & 1)
t = Add(t, a);
a <<= 1;
if ((b >> 1) == b) // b가 INT_MIN으로 들어온 경우 >> 반복해도 항상 INT_MIN이기에 예외처리
break;
b >>= 1;
}
if (negativeResult)
t = ~t + 1;
a = t;
return a;
}음수인경우 예외처리 같은 짜잘한 부분은 제치고 메인인 while문을 봐주시기 바랍니다.
2진수 곱셈 과정 또한 10진수 곱셈 과정하고 같습니다.
15와 27의 곱셈 과정을 풀어 보겠습니다.
15
x 27
--------
15
15
15
15
15
15
15
--------
105
15
15
--------
405곱셈은 다들 아시다시피
A를 B번 더하는것 입니다.
따라서 15 * 27은 15를 27번 더한것이죠
곱셈 과정을 보시면 처음에 15를 7번 더하고
십의 자리수인 2번 만큼 또 15를 더해주는데 이때 십의 자리이기 때문에
15는 한칸 앞으로 땡기고 20은 뒤로 땡겨서 2로 만든뒤 150을 2번 더한다면
150 + 150 이 되게 됩니다.
단순하게 표현하면 아래와 같습니다.
15 * 7 = 105
150 * 2 = 300
105 + 300 = 405
이 과정을 정리해보면
곱셈 과정
- A를 B번 더하는것이 곱셈
- B의 일의 자리수만큼 A를 더한다.
- 더한 뒤 B의 B가 0이 아니라면 A를 10 곱하고 B를 10 나눈다.
- 2-3을 반복한다.
똑같이 15와 27을 2진수로 위 곱셈과정을 적용하여 곱해보겠습니다.
(각각 1111, 11011)
1111
x 11011
----------
1111
1111
----------
101101
1111
----------
10100101
1111
----------
110010101 // 405곱셈 과정을 보시면 10진수를 기준으로 말씀 드렸기에
10을 곱하고 나누는 부분을 2를 곱하고 나누는것으로 재해석 하면 됩니다.
보시면
a * b^0 == 1111
a * b^1 == 11110
( a * b^1 ) + ( a * b^0 ) = 101101
으로 되었는데 a * b^1 부분에서 11110이 된것을 곱셈과정 똑같이 적용해 보세요.
- (a * 2) * (b^1 / 2)
- (11110) * (1)
- 11110
와우! 똑같이 11110이 나왔네요
이 값을 전 곱셈 과정 결과인 1111과 더하고
101101이 되고 b^2, b^3 ... 또한 같은 방식으로 곱셈 연산을 하면 됩니다.
다시 본문인 while 반복문 코드로 돌아가보면
b & 1로 현재 곱해야 하는지를 체크한뒤
a를 왼쪽, b를 오른쪽 쉬프트 연산을 해줍니다.
b가 0이 아닐 때까지 반복해주면 곱셈연산 끝입니다.
두 수를 양수화 시키는 이유는 단순히 계산하기 편하니까 입니다.
큰 이유 없습니다.
5. 나눗셈 구현
10진수 나눗셈 과정과 2진수 나눗셈 과정은 완전히 같습니다.
10진수 나눗셈 과정
- 제수가 피제수 이하이면서 가장 근접한 값을 가질 때까지 10을 곱한다.
- 제수에 10을 곱했던 반복횟수만큼 1을 10씩 곱한다.
- 피제수를 곱한 제수만큼 반복해서 뺀다.
- 1을 10씩 곱한 수 * 뺀 횟수를 몫에 더한다
- 제수가 피제수보다 작을 때까지 1-4을 반복한다.
2진수 나눗셈이라면 여기서 10을 2로 바꾸면 됩니다.
그 식을 적용해서 한번 풀어봅시다.
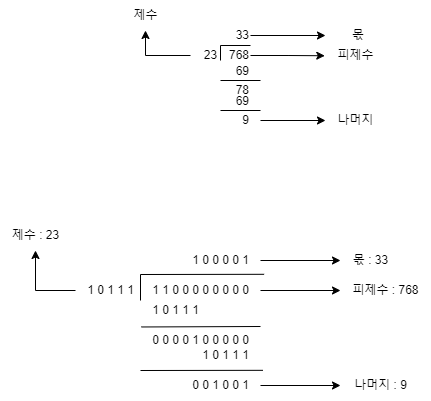
해당 사진에서 쓰인 나눗셈 식은 long division 이라고 해서 저희가 학교에서 흔히 배웠던 나눗셈 방식 중 하나입니다.
보시면 768 / 23 을 하는데 10진수와 2진수의 나눗셈 과정이 똑같죠?
2진수 쪽 나눗셈 보시면 10111이 768의 2진수보다 작으면서 최대한 근접한 값을 가질 때 까지 2를 곱해 왼쪽으로 이동시킨뒤 빼주는걸 반복하고 제수가 피제수보다 크니 종료되는것이죠.
위쪽에서 설명드린 나눗셈 과정을 보시고 오면 이해가 잘 되실겁니다.
int Divide(int* a, int b) { // a를 나머지로 사용하기에 *a 로 받음
if (b == 0)
{
fprintf(stderr, "Error : Division by zero"); // 0으로 나눌 시 예외처리
exit(1);
}
if (*a == INT_MIN && b == INT_MIN) { // 둘 다 INT_MIN 인경우 예외처리
*a = 0;
return 1;
}
if (b == INT_MIN) // 나누는수가 INT_MIN이고 나눌 수가 INT_MIN이 아니면 몫은 0, 나머지는 a 그대로
return 0;
if (*a == INT_MIN) {
if (b == -1) { // INT_MIN / -1 오버플로우 예외 처리
fprintf(stderr, "Error : Integer Overflow");
exit(1);
}
int t = HALF_INT_MIN; // INT_MIN / 2
if (abs(b) > abs(t)) { // b의 절댓값이 INT_MIN / 2 (2^30)절댓값보다 큰 경우
*a = Add(*a, abs(b));
if (b < 0)
return 1;
return -1;
}
int n = Divide(&t, b);
n = Multiply(n, 2);
t = Multiply(t, 2); // (INT_MIN / b) == (((INT_MIN / 2) / b) * 2)
if (abs(t) >= abs(b)) { // 몫과 나머지 정리
n = Add(n, 1);
t = -(abs(t) - abs(b));
}
*a = t;
return n;
}
bool negativeResult = false;
if ((*a < 0 && b > 0) || (*a > 0 && b < 0))
negativeResult = true;
bool negativeA = *a < 0;
*a = abs(*a);
b = abs(b);
int ret = 0;
while (*a >= b) {
int t1 = b;
int t2 = 1;
while (*a >= (t1 << 1) && (t1 << 1) > 0) {
t1 <<= 1;
t2 <<= 1;
}
ret = Add(ret, t2);
*a = Subtract(*a, t1);
}
if (negativeResult)
ret = -ret;
if (negativeA)
*a = -*a;
return ret;
}짜잘한 예외처리는 제치고 중요한 while을 보시면
반복문에 들어오기전 절댓값으로 바꿔준뒤 제수가 피제수보다 작을 때까지 반복합니다.
이후 제수의 값과 1이란 값을 변수2개에 넣어준 뒤
제수 이하이면서 최대한 근접한 값을 가질때까지 두 변수를 왼쪽 시프트를 해줍니다.
(t1 << 1) > 0은 부호비트 오버플로우 방지 조건
이후 시프트된 두 변수를 각각 결과값(몫)에 더하고 피제수(나머지)를 빼주는걸 반복한뒤
각각 조건에 맞게 음수부호로 바꾼 뒤 반환하면 됩니다.
참고자료
https://www.youtube.com/watch?v=VKemv9u40gc&ab_channel=NesoAcademy
https://www.youtube.com/watch?v=xHWKYFhhtJQ&t=100s&ab_channel=KhanAcademy
'C' 카테고리의 다른 글
| [C언어] 함수 포인터 개념과 활용 (0) | 2024.08.28 |
|---|---|
| [C] strdup, strjoin, split 구현 (0) | 2023.12.05 |
| [C] strcmp / strncmp / memcmp 사용법과 구현 및 strncmp와 memcmp의 차이 (0) | 2023.02.11 |
| [C] strcat / strncat / strlcat 사용법과 구현 (0) | 2023.02.04 |
| [C] strlen / strcpy / strncpy / strlcpy 사용법과 구현 (0) | 2023.02.02 |
※사칙 연산(+, -, *, /)만 다룹니다.
논리회로는 귀찮아서 따로 그리지 않았습니다.
1. 반가산기와 전가산기
컴퓨터는 전가산기를 통해 덧셈을 수행합니다.
그 과정에서 반가산기를 사용하기에 반가산기를 포함하여 설명드립니다.
이진수 덧셈과 십진수 덧셈은 다를게 없습니다.
10진수 두 수 7과 4가 있다고 칩시다.
이 두 수의 이진수 덧셈과 십진수 덧셈과정을 봅시다.
각 수를 A와 B라고 부르겠습니다.
10진수인 경우
- A, B 각각 일의 자리부터 더한다.
- A의 현재 자릿수에 1을 B의 현재 자리수만큼 덧셈을 반복한다.
- 더하는 도중 현재 자릿수가 9를 초과할 시 현재 자릿수를 0으로 만들고 다음 자릿수를 1올림한다. (올림 발생)
- 올림 발생 후 나머지를 더한다.
이 네가지대로 더한다면 A가 7이고 B가 4니까
7에 1을 4번 더하는거니까
3번에서 나온것처럼 10이 되고
4번을 수행하면 11이 됩니다.
만약 A가 15여서 한쪽만 자릿수가 더 높아서 B의 십의 자리가 없다면?
A의 십의 자리에 B의 십의 자리를 0만큼 더하면 됩니다.
10진수에서 했던것 처럼 현재 자릿수 덧셈 공식을 똑같이 적용해봅시다.
2진수인 경우 (0111, 0100)
- A^0 와 B^0을 더한다(1 + 0) → 1
- A^1 와 B^1을 더한다(1 + 0) → 1
- A^2 와 B^2을 더한다(1 + 1) → 0 (올림 발생)
- A^3 와 B^3을 더한다(0 + 0 + 이전 올림) → 1
- 결과 1011 → 10진수 11
이 과정을 좀더 깊게 살펴봅시다.
| 7 | 4 | 합 | 올림 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
표를 보면 합이 0011, 올림이 0100이 됩니다.
합은 어떤 비트연산을 써야할까요?
XOR를 사용하면 될것 같군요. 따라서 식은 A ^ B가 되겠습니다.
올림은 어떤 비트연산을 써야할까요?
AND를 사용하면 될것 같군요. 따라서 식은 A & B가 되겠습니다.
그럼 10진수도 똑같이 해볼까요?
347과 921이 있다고 칩시다.
| 347 | 921 | 합 | 올림 |
| 7 | 1 | 8 | 0 |
| 4 | 2 | 6 | 0 |
| 3 | 9 | 2 | 1 |
| 0 | 0 | 0 | 0 |
여기서 똑같이 올림이 발생했으니 다음 자릿수로 올림을 적용하면?
1268 이라는 결과값이 나오게 됩니다!
2진수와 덧셈과정이 왜 똑같다는지 아시겠죠??
자 그럼 방금 보셨던 내용이 반가산기인데요.
반가산기(半加算器, half adder)는 이진수의 한자리수를 연산하고, 자리올림수는 자리올림수 출력(carry out)에 따라 출력한다. AND, OR, NOT의 세 가지 종류의 논리회로만으로 구성할 수 있다.
왜 반가산기(Hallf Adder)라고 불릴까요??
이유는 올림만 있지 그 올림을 실제로 적용시키지는 않기 때문인데요.
이제 올림을 실제로 적용시키는 전가산기의 과정을 봅시다.
전가산기 과정
- A와 B를 반가산기로 더한다.
- 반가산기로부터 나온 합(S)과 올림(C)을 반가산기로 더한다.
- 올림이 없을때까지 1-2를 반복한다.
자 이 과정을 표로 표현해봅시다.
| 7 | 4 | 이전 올림(Cin) | 합(S) | 올림(Cout) |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
첫 행부터 봐봅시다.
첫 번째 행 1 0 0 이기에 합이 1 올림 0
두 번째 행 1 0 0 이기에 합이 1 올림 0
세 번째 행 1 1 0 이기에 합이 0 올림 1
네 번째 행 0 0 1 이기에 합이 1 올림 0
최종 합 1011이 나오게 되는데
맨 처음 이전 올림은 당연히 없으니까 0
네 번째 행인 2^3 번째는 이전 올림이 있었기에 1이 되었죠
전가산기 과정 2번을 보면 합과 올림을 반가산기로 더한다는게
이전 올림(Cin)과 반가산기 합의 공식 A ^ B를 합하라는 것입니다.
여기서의 합의 공식은 A ^ B ^ Cin이 되겠습니다.
그렇다면 올림은 어떻게 될까요?
| A | B | 이전 올림(Cin) | 합(S) | 올림(Cout) |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
전가산기의 진리표입니다.
여기서의 이전 올림은 표의 현재 올림과 상관없습니다.
올림 공식을 어떻게 짜면 좋을까요?
처음 반가산기에서의 올림 공식은 A & B이었습니다.
유심히 살펴보면 A, B, Cin 이 셋중 두개 이상 1인 경우 올림이 발생합니다.
식으로 유도해보면
Cout = (A & B) | (A & C) | (B & C)
이렇게 식을 짤 수 있습니다.
따라서 합과 올림의 식은 다음과 같습니다.
S = A ^ B ^ Cin
Cout = A & B | A & C | B & C
2. 덧셈 구현
int Add(int a, int b) {
while (b != 0) {
int c = a & b;
a = a ^ b;
b = c << 1;
}
return a;
}c를 올림으로 사용하고
a를 합으로 사용하고
b를 마지막에 이전 올림을 적용 시켜줍니다.
이 과정을 반복하면 일반 + 연산과 동일한 기능을 하게되는데요.
설명드렸던 전가산기 과정을 보시면
- A, B를 반가산기로 더한다.
- 나온 합과 이전 올림을 더한다.
- 올림이 없을 때까지 반복한다.
int c = a & b가 올림
a = a ^ b 가 합
b = c << 1이 올림 적용
흐음.. Cin이 어디에 있는거지?? 라는 생각이 들면
while 2번째 부터 생각해 보세요
a는 이전 합을 구했고
b는 이전 올림을 적용한 상태입니다.
그래서 두 번째 반복부터 S = (a(A ^ B) ^ b(Cin)) 형태로써 완벽하게 합을 구할 수 있게 되는것이죠
이 과정을 b가 0이 아닐때 까지 == 올림이 없을 때까지 반복하면 덧셈 구현 끝입니다!
3. 뺄셈 구현
int Subtract(int a, int b) {
return Add(a, -b);
}뺄셈은 간단하죠 b를 음수로 만든 뒤 더하면 끝입니다.
물론 비트연산을 사용해 다르게 구현할 수 있습니다.
int Subtract(int a, int b) {
return Add(a, ~b + 1);
}다르게 구현하면 이 방식으로 구현할 수 있는데요
~ 기호는 not으로써 모든 0비트를 1로, 모든 1비트를 0으로 바꿉니다.
따라서 양수인 수는 음수, 음수인 수는 양수가 되는데요.
그렇다면 왜 1을 더하는가?
int 자료형의 범위를 보면 -2,147,483,648 ~ 2,147,483,647
최소값과 최대값이 절댓값 적용했을 때 1차이가 납니다.
그 이유는 0이 양수쪽에 포함되어있기 때문입니다.
따라서 not을 적용했을 때 1의 오차가 포함되어있기 때문에 1을 더해주면
~b + 1 == -b 식과 같기 때문에 a + ~b + 1을 해주면 뺄셈 구현 끝입니다.
4. 곱셈 구현
int Multiply(int a, int b) {
bool negativeResult = false;
if ((a < 0 && b > 0) || (a > 0 && b < 0))
negativeResult = true;
a = abs(a);
b = abs(b);
int t = 0;
while (b != 0) {
if (b & 1)
t = Add(t, a);
a <<= 1;
if ((b >> 1) == b) // b가 INT_MIN으로 들어온 경우 >> 반복해도 항상 INT_MIN이기에 예외처리
break;
b >>= 1;
}
if (negativeResult)
t = ~t + 1;
a = t;
return a;
}음수인경우 예외처리 같은 짜잘한 부분은 제치고 메인인 while문을 봐주시기 바랍니다.
2진수 곱셈 과정 또한 10진수 곱셈 과정하고 같습니다.
15와 27의 곱셈 과정을 풀어 보겠습니다.
15
x 27
--------
15
15
15
15
15
15
15
--------
105
15
15
--------
405곱셈은 다들 아시다시피
A를 B번 더하는것 입니다.
따라서 15 * 27은 15를 27번 더한것이죠
곱셈 과정을 보시면 처음에 15를 7번 더하고
십의 자리수인 2번 만큼 또 15를 더해주는데 이때 십의 자리이기 때문에
15는 한칸 앞으로 땡기고 20은 뒤로 땡겨서 2로 만든뒤 150을 2번 더한다면
150 + 150 이 되게 됩니다.
단순하게 표현하면 아래와 같습니다.
15 * 7 = 105
150 * 2 = 300
105 + 300 = 405
이 과정을 정리해보면
곱셈 과정
- A를 B번 더하는것이 곱셈
- B의 일의 자리수만큼 A를 더한다.
- 더한 뒤 B의 B가 0이 아니라면 A를 10 곱하고 B를 10 나눈다.
- 2-3을 반복한다.
똑같이 15와 27을 2진수로 위 곱셈과정을 적용하여 곱해보겠습니다.
(각각 1111, 11011)
1111
x 11011
----------
1111
1111
----------
101101
1111
----------
10100101
1111
----------
110010101 // 405곱셈 과정을 보시면 10진수를 기준으로 말씀 드렸기에
10을 곱하고 나누는 부분을 2를 곱하고 나누는것으로 재해석 하면 됩니다.
보시면
a * b^0 == 1111
a * b^1 == 11110
( a * b^1 ) + ( a * b^0 ) = 101101
으로 되었는데 a * b^1 부분에서 11110이 된것을 곱셈과정 똑같이 적용해 보세요.
- (a * 2) * (b^1 / 2)
- (11110) * (1)
- 11110
와우! 똑같이 11110이 나왔네요
이 값을 전 곱셈 과정 결과인 1111과 더하고
101101이 되고 b^2, b^3 ... 또한 같은 방식으로 곱셈 연산을 하면 됩니다.
다시 본문인 while 반복문 코드로 돌아가보면
b & 1로 현재 곱해야 하는지를 체크한뒤
a를 왼쪽, b를 오른쪽 쉬프트 연산을 해줍니다.
b가 0이 아닐 때까지 반복해주면 곱셈연산 끝입니다.
두 수를 양수화 시키는 이유는 단순히 계산하기 편하니까 입니다.
큰 이유 없습니다.
5. 나눗셈 구현
10진수 나눗셈 과정과 2진수 나눗셈 과정은 완전히 같습니다.
10진수 나눗셈 과정
- 제수가 피제수 이하이면서 가장 근접한 값을 가질 때까지 10을 곱한다.
- 제수에 10을 곱했던 반복횟수만큼 1을 10씩 곱한다.
- 피제수를 곱한 제수만큼 반복해서 뺀다.
- 1을 10씩 곱한 수 * 뺀 횟수를 몫에 더한다
- 제수가 피제수보다 작을 때까지 1-4을 반복한다.
2진수 나눗셈이라면 여기서 10을 2로 바꾸면 됩니다.
그 식을 적용해서 한번 풀어봅시다.

해당 사진에서 쓰인 나눗셈 식은 long division 이라고 해서 저희가 학교에서 흔히 배웠던 나눗셈 방식 중 하나입니다.
보시면 768 / 23 을 하는데 10진수와 2진수의 나눗셈 과정이 똑같죠?
2진수 쪽 나눗셈 보시면 10111이 768의 2진수보다 작으면서 최대한 근접한 값을 가질 때 까지 2를 곱해 왼쪽으로 이동시킨뒤 빼주는걸 반복하고 제수가 피제수보다 크니 종료되는것이죠.
위쪽에서 설명드린 나눗셈 과정을 보시고 오면 이해가 잘 되실겁니다.
int Divide(int* a, int b) { // a를 나머지로 사용하기에 *a 로 받음
if (b == 0)
{
fprintf(stderr, "Error : Division by zero"); // 0으로 나눌 시 예외처리
exit(1);
}
if (*a == INT_MIN && b == INT_MIN) { // 둘 다 INT_MIN 인경우 예외처리
*a = 0;
return 1;
}
if (b == INT_MIN) // 나누는수가 INT_MIN이고 나눌 수가 INT_MIN이 아니면 몫은 0, 나머지는 a 그대로
return 0;
if (*a == INT_MIN) {
if (b == -1) { // INT_MIN / -1 오버플로우 예외 처리
fprintf(stderr, "Error : Integer Overflow");
exit(1);
}
int t = HALF_INT_MIN; // INT_MIN / 2
if (abs(b) > abs(t)) { // b의 절댓값이 INT_MIN / 2 (2^30)절댓값보다 큰 경우
*a = Add(*a, abs(b));
if (b < 0)
return 1;
return -1;
}
int n = Divide(&t, b);
n = Multiply(n, 2);
t = Multiply(t, 2); // (INT_MIN / b) == (((INT_MIN / 2) / b) * 2)
if (abs(t) >= abs(b)) { // 몫과 나머지 정리
n = Add(n, 1);
t = -(abs(t) - abs(b));
}
*a = t;
return n;
}
bool negativeResult = false;
if ((*a < 0 && b > 0) || (*a > 0 && b < 0))
negativeResult = true;
bool negativeA = *a < 0;
*a = abs(*a);
b = abs(b);
int ret = 0;
while (*a >= b) {
int t1 = b;
int t2 = 1;
while (*a >= (t1 << 1) && (t1 << 1) > 0) {
t1 <<= 1;
t2 <<= 1;
}
ret = Add(ret, t2);
*a = Subtract(*a, t1);
}
if (negativeResult)
ret = -ret;
if (negativeA)
*a = -*a;
return ret;
}짜잘한 예외처리는 제치고 중요한 while을 보시면
반복문에 들어오기전 절댓값으로 바꿔준뒤 제수가 피제수보다 작을 때까지 반복합니다.
이후 제수의 값과 1이란 값을 변수2개에 넣어준 뒤
제수 이하이면서 최대한 근접한 값을 가질때까지 두 변수를 왼쪽 시프트를 해줍니다.
(t1 << 1) > 0은 부호비트 오버플로우 방지 조건
이후 시프트된 두 변수를 각각 결과값(몫)에 더하고 피제수(나머지)를 빼주는걸 반복한뒤
각각 조건에 맞게 음수부호로 바꾼 뒤 반환하면 됩니다.
참고자료
https://www.youtube.com/watch?v=VKemv9u40gc&ab_channel=NesoAcademy
https://www.youtube.com/watch?v=xHWKYFhhtJQ&t=100s&ab_channel=KhanAcademy
'C' 카테고리의 다른 글
| [C언어] 함수 포인터 개념과 활용 (0) | 2024.08.28 |
|---|---|
| [C] strdup, strjoin, split 구현 (0) | 2023.12.05 |
| [C] strcmp / strncmp / memcmp 사용법과 구현 및 strncmp와 memcmp의 차이 (0) | 2023.02.11 |
| [C] strcat / strncat / strlcat 사용법과 구현 (0) | 2023.02.04 |
| [C] strlen / strcpy / strncpy / strlcpy 사용법과 구현 (0) | 2023.02.02 |
