문제
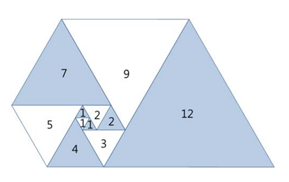
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
예제 입력 1
2
6
12
예제 출력 1
3
16
문제 파악
1, 1, 1, 2, 2, 3, 4, 5, 7, 9 같은 식으로 수열이 생기는데 P(N)값을 출력하라는 문제이다.
N이 6이면 P(6) = 3이 된다.
수열을 자세히 보면 규칙이 보인다.그 규칙을 점화식으로 짜보면 다음과 같다.
P(N) = P(N - 2) + P(N - 3)이 점화식이 맞는지는 적당히 검증해보면 된다.
간단하게 예제 입력과 출력으로 검증을 해보자
N이 6일 때는
P(6) = P(4) + P(3)
= P(6) = 2 + 1
= P(6) = 3
N이 12일 때는
P(12) = P(10) + P(9)
= P(12) = 9 + 7
= P(12) = 16
적당히 검증이 된것 같으니 코드를 짜고 제출해보니
정답이나왔다
코드
#include <string>
#include <iostream>
#include <vector>
using namespace std;
int main()
{
long long T;
cin >> T;
vector<long long> vec;
vec.assign(100, 0);
vec[0] = 1;
vec[1] = 1;
vec[2] = 1;
for (long long j = 3; j < 100; j++)
vec[j] = vec[j - 2] + vec[j - 3];
for (long long i = 0; i < T; i++)
{
long long N;
cin >> N;
cout << vec[N - 1] << endl;
}
}dp문제이니 간단하게 바텀업으로 구현했다.
맨 처음 점화식을 그대로 적용시켜 벡터에 저장한뒤
N을 입력받아 그대로 출력시켰다.
int가 아닌 8바이트짜리 longlong으로 해줘야 정답이 나올것이다.
'백준 C++' 카테고리의 다른 글
| [C++] 백준 17626 Four Squares (0) | 2025.04.16 |
|---|---|
| [C++] 백준 9375 패션왕 신해빈 (0) | 2025.04.07 |
| [C++] 백준 11723 집합 (0) | 2024.11.22 |
| [C++] 백준 2885 초콜릿 식사 (0) | 2024.07.08 |
문제

오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
예제 입력 1
2
6
12
예제 출력 1
3
16
문제 파악
1, 1, 1, 2, 2, 3, 4, 5, 7, 9 같은 식으로 수열이 생기는데 P(N)값을 출력하라는 문제이다.
N이 6이면 P(6) = 3이 된다.
수열을 자세히 보면 규칙이 보인다.그 규칙을 점화식으로 짜보면 다음과 같다.
P(N) = P(N - 2) + P(N - 3)이 점화식이 맞는지는 적당히 검증해보면 된다.
간단하게 예제 입력과 출력으로 검증을 해보자
N이 6일 때는
P(6) = P(4) + P(3)
= P(6) = 2 + 1
= P(6) = 3
N이 12일 때는
P(12) = P(10) + P(9)
= P(12) = 9 + 7
= P(12) = 16
적당히 검증이 된것 같으니 코드를 짜고 제출해보니
정답이나왔다
코드
#include <string>
#include <iostream>
#include <vector>
using namespace std;
int main()
{
long long T;
cin >> T;
vector<long long> vec;
vec.assign(100, 0);
vec[0] = 1;
vec[1] = 1;
vec[2] = 1;
for (long long j = 3; j < 100; j++)
vec[j] = vec[j - 2] + vec[j - 3];
for (long long i = 0; i < T; i++)
{
long long N;
cin >> N;
cout << vec[N - 1] << endl;
}
}dp문제이니 간단하게 바텀업으로 구현했다.
맨 처음 점화식을 그대로 적용시켜 벡터에 저장한뒤
N을 입력받아 그대로 출력시켰다.
int가 아닌 8바이트짜리 longlong으로 해줘야 정답이 나올것이다.
'백준 C++' 카테고리의 다른 글
| [C++] 백준 17626 Four Squares (0) | 2025.04.16 |
|---|---|
| [C++] 백준 9375 패션왕 신해빈 (0) | 2025.04.07 |
| [C++] 백준 11723 집합 (0) | 2024.11.22 |
| [C++] 백준 2885 초콜릿 식사 (0) | 2024.07.08 |
